
I don't have anything to share yet since I can't get my copy for another couple hours, but if you have designed or by other means discovered an awesome design for a t-shirt, wallpaper, or whatever, go ahead and post it here.
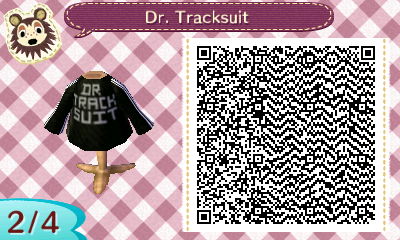
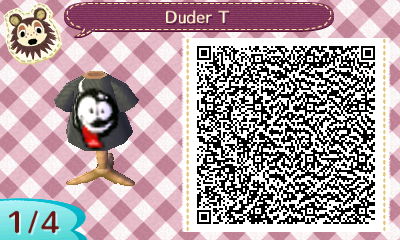
I'm sure we could get some pretty cool recreations of GB shirts and other GB-related stuff.
Or if you want to design stuff the old fashioned way and post it, feel free to do that too. All designs are 32 x 32 pixels.























































Log in to comment